Idea: I want to create a combinatory logic which gives rise to efficient programs that are capable of recognising the a^nb^n language. I want to study if shorter programs (low Kolmogorov complexity) generalise better than longer programs (high Kolmogorov complexity).

What is a combinatory logic?

A combinatory logic is a simplified model of computation, an early rival to lambda calculus. In expressiveness, it is equivalent to the lambda calculus, but less human readable, given that it does away with variables and abstraction.

Formally, it is a set A equipped with operators of signature A^m -> A. That is, we take an ordered tuple of m elements from A and assign an element of A as a result. A famous example is the SKI combinator calculus, where we require S, K and I to satisfy the following relations (I use the @ sign to mean application):

1. I @ x = x
2. K @ x @ y = x
3. S @ x @ y @ z = x @ z @ (y @ z).

We call this SKI basis Turing complete because we can take any lambda calculus term and find an equivalent element in the SKI combinator calculus. The translation function (i.e., the “compiler”) is also well-defined. This is well known, but I have written about it in a previous post.

Why would it be interesting to do Solomonoff Induction on combinatory logics?

Universal AI and Solomonoff Induction are famously hard to implement. Solomonoff Induction when done on Turing Machines is uncomputable, although approximable. However, the goal we set off for ourselves is to recognise the a^nb^n language, which is only context-free (2 levels below Turing Machines in the Chomsky Hierarchy). Would it be possible to first synthesise a combinatory logic that is perhaps less expressive than SKI but still powerful enough to give rise to useful programs that recognise a^nb^n? Perhaps Solomonoff Induction becomes efficient in such a reduced setting?

Starting point

So what do we need? In principle, I want to find a program P that when applied to an input w (this input comes from the {a,b}* set) terminates with a 0 element F — F for false — if and only if w is not in the a^nb^n language and terminates with T — T for true — otherwise.

We need a way to represent inputs. Any combinatory logic we find will have A = { a, b, F, T, … }. We either allow A to have elements from {a,b}* or we equip it with a combinator representing concatenation of elements. I want to go with the latter approach here, let’s call this combinator C. Concatenation would typically take two arguments, so you would write it as C(w1, w2), but you only have a single application operator in combinatory logics. Associativity applies to concatenation, so you can write C(C(w1, w2), w3) = C(w1, C(w2, w3)):

1. C @ (C @ w1 @ w2) @ w3 = C @ w1 @ (C @ w2 @ w3)

A little example. The following rewrite system is not Turing complete, but recognises a^nb^n:

1. C @ a @ b = T
2. C a @ (C @ T @ b) = T.

Intuitively, these two rules implement the following rewrite system:

1. ab -> T
2. aTb -> T.

In this system only a^nb^n reduces to T. Everything else will “get stuck”.

How to find the rules?

A computer program capable of finding such a combinatory logic would need to:

1. either invent C or be told about it¹,
2. assign the special meaning to T that it represents “ab balance”,
3. find that aTb does not change the balance.

This portrays this computer program way too intelligent. We should formalise what the search space looks like over rewrite rules, or, in our case, combinatory logic identities. Really, they are just trees. Here is the first rewrite rule pictorially:

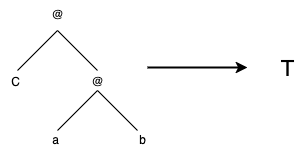
The second rule looks like this:

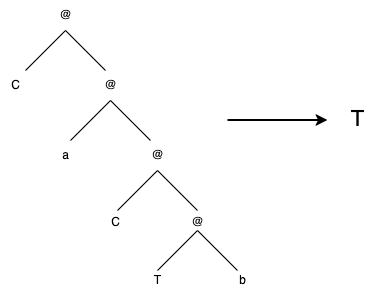
Now, we get to define our task more formally.

Task: I seek to find the least complex List[RewriteRule] that recognises a^nb^n in the least number of steps on average².

Here, RewriteRule is:

RewriteRule = Rule of Left * Right
Left = TreeExpression
Right = TreeExpression

TreeExpression =
| A | B | T | C
| At of TreeExpression * TreeExpression

How should we traverse the search space?

Without overthinking too much, the simplest brute-force search algorithm would do something like this:

1. Generate a random number N. This will be the number of rewrite rules we work with.
2. N times: generate a random TreeExpression for the left-hand side, generate a random right-hand side. Optionally, if we want terminating or non-growing rewrite systems, make sure that the right-hand side is smaller or not bigger than the left-hand side.
3. Run this rewrite system on a set of test cases pre-prepared. If a test case runs too long, terminate it and fail the test case. Measure how many times the output was correctly T. Measure how many times a rule was used in successful/non-successful program executions. Measure the contribution of each rule to the score of the rewrite system.

Questions:

1. How to generate random TreeExpressions? What is a useful parameterisation? We need feedback from the score and be able to adjust this parameterisation.

References

1. https://en.wikipedia.org/wiki/Combinatory_logic
2. https://en.wikipedia.org/wiki/SKI_combinator_calculus
3. https://en.wikipedia.org/wiki/Kleene_star

Footnotes

1. Here, we would probably want to predefine C as part of our system. Otherwise, we would not be able to provide inputs to programs. ↩︎
2. “Least complex” and “least number of steps” still require definition, but let us make progress. ↩︎